Perturbation Solution of![]()
Find an approximate solution of![]()
as![]()
The equation obviously has an analytical solution, so the purpose
here is to demonstrate the perturbation method on an equation with
a known solution, so that we can see that the method works.
![]()
First, define the equation:
![]()
![]()
Find the exact solutions, which comes out as a list of 2 replacment rules:
![]()
![]()
Show how to access the element of a list (in case you do not know):
![]()
![]()
![]()
![]()
Check that these solutions really do satisfy qe:
![]()
![]()
![]()
![]()
Define functions x(ε)for the two exact, analytical solutions
![]()
![]()
![]()
![]()
Now prepare to find an approximate perturbation solution. Note
the O[ε] symbol is powerful in Mathematica, try changing {n,0,2} to {n,0,10) and see what happens...
![]()
![]()
Substitute the series solution for xinto the equation qe:
![]()
![]()
LogicalExpand is really cool, and works because of the presence of the O[ε] symbol :
![]()
![]()
The "logical and" might just as well be a list of equations that need to be true. In fact the equation can be accessed as list, for example:
![]()
![]()
![]()
![]()
So here are the two approximate solutions to qe:
![]()
![]()
![]()
![]()
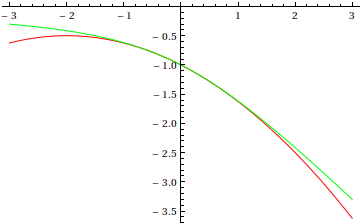
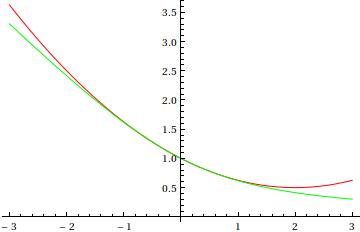
Compare the exact (green) and approximate (red) solutions:
![]()
![]()