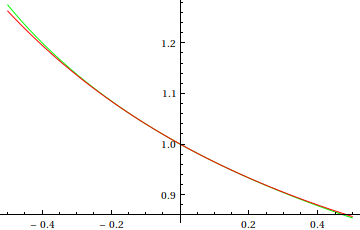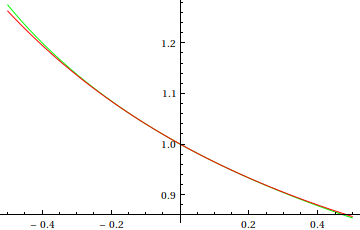A Nonlinear Oscillator,
Numerical Solution
Problem 3, on P.S. #3, 2002. Numerical check of perturbation
solution, problem not solved here.
Finds a numerical solution to:
y'' + y 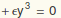
with y'(0)=0 and y(0)=1.
The period in the numerical solution is then compared to the prediction made from the perturbation expansion. The math for the
perturbation expansion is not shown here.
In[1]:=
The following line was changed to text. You may want to change the Format>Style to "Input" to execute the statement, and confirm that Mathematica cannot find an analytical solution:
DSolve[{y''[t]+y[t]+eps*y[t]^3==0,y[0]==1,y'[0]==0},y[t],t]
So we resort to a numerical solution for a specified value of eps:
In[2]:=
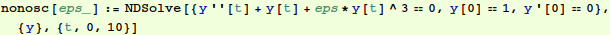
In[3]:=
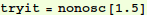
Out[3]=
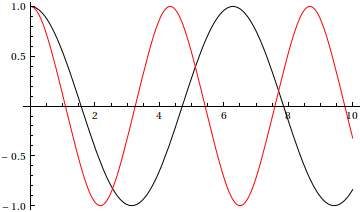
Plot the analytical solution for eps=0 in black and the numerical
solution for eps=0.5 in red:
In[4]:=
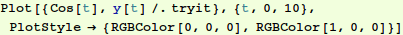
Out[4]=
Here we make a more convenient interface to access the interpolating function that contains the numerical solution. Notice the replacement rule is inside a nested list, which is accessed by the [[1,1]]:
In[5]:=
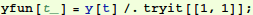
Let's give it a try:
In[6]:=
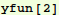
Out[6]=
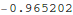
Let's find t where y(t)=0 in the numerical solution:
In[7]:=
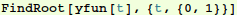


Out[7]=
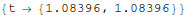
Now make a module to find the first t where y(t)=0 for a
specified value of ε.
In[8]:=

Try it:
In[9]:=
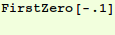
Out[9]=
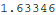
In[10]:=
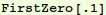
Out[10]=
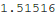
Make a table of ratio of the period of oscillation to that with ε=0.
In[11]:=
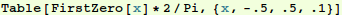
Out[11]=
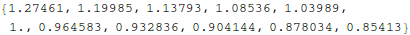
In[12]:=
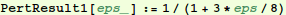
In[13]:=
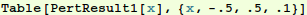
Out[13]=
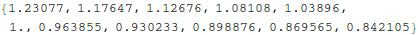
Compare the numerical result, which we assume to be exact, (green) with the perturbation result (red).
In[14]:=
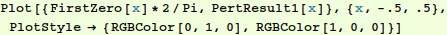
Out[14]=
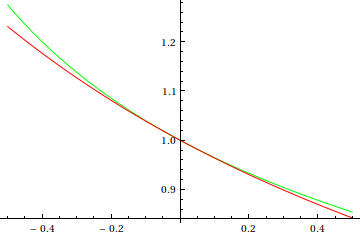
Now compare with the perturbation result out to 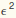 :
:
In[15]:=
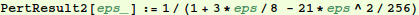
In[16]:=
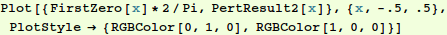
Out[16]=