Regular Power Series Solution
Solution of
y''+cos(x) y=0
for y(x) with y(0)=1 and y'(0)=0.
An exact solution can be found in this case, and can
be compared with the series solution.
In[1]:=
Let's find a solution valid out to 
. The first step in finding a series solution is to find an expansion for Cos[x]:
In[2]:=
In[3]:=
Out[3]=
In[4]:=
Out[4]=
In[5]:=
Out[5]=
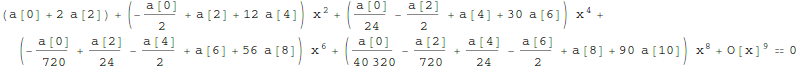
Here are the unknowns in the expansion of y(x) that we must solve for:
In[6]:=
Out[6]=
Here are the algebraic equations for those coefficients:
In[7]:=
Out[7]=
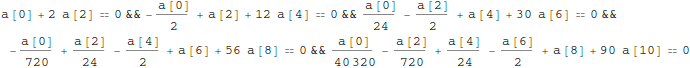
We actually don't need the TableForm for the math, it is just nice to look at:
In[8]:=
Out[8]//TableForm=
| a[0]+2 a[2]==0 |
 |
 |
 |
 |
In[9]:=
Out[9]=
In[10]:=
Out[10]=
In[11]:=
Out[11]=
So here is the series solution that satisfies the specified initial conditions:
In[12]:=
Out[12]=
Now find exact solution:
In[13]:=
In[14]:=
Out[14]=
In[15]:=
Out[15]=
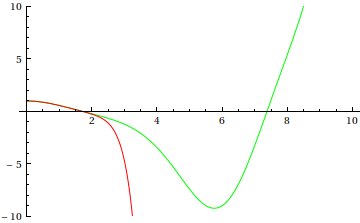
Plot approximate (red) and exact (green) solutions:
In[16]:=
Out[16]=
