 |
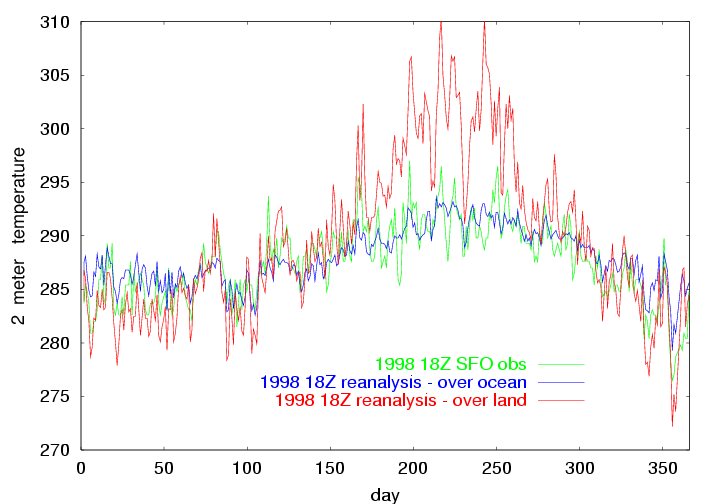
The above image shows the 1998 18Z observation of temperature at SFO, and the NCEP 18Z reanalysis at the ocean point just to the west of SFO, and the NCEP 18Z reanalysis at the land point just to the east of SFO. |
|
A Neural Network AMOS for SFO surface air temperature |
| This page was revised and upgraded on April 4, 2001. |
This page shows an example of using the backpropagation algorithm coded
in my neural network freeware v0.41 in the construction
of a nonlinear advanced model output statistics (AMOS) for the 18Z surface
air temperature at San Francisco Airport (SFO). The goal of the AMOS is
to predict the observed surface air temperature at SFO at 18Z from the
data in the 12Z files. The NCEP reanalysis for the boundary layer is actually
a six hour forecast. The 18Z forecast is stored in files timestamped as
12Z. (It is my understanding that surface obs are not actually used in
this forecast.) In other words, we are finding the model bias in the reanalysis
forecast for the boundary layer. The readily available reanalysis provides
a useful proxy as a forecast system, at least for an academic exercise.
A less successful application of this technique can be found at:
Statistical prediction of SFO summer burnoff
After you have successfully installed neural network freeware v0.41, this entire exercise can be reproduced by simply executing the run script dothis within the download sfoamos.tar.gz. Within sfoamos you will find two large files of data: sfo_18Z_obs.dat and sforean.dat. The toils of preparing the SFO observational data contained within sfo_18Z_obs.dat can be reproduced with sfodata.tar.gz (10Mb). The details of how to prepare sforean.dat may be found at An Archive of NCAR/NCEP Reanalysis Data.
 |
The above image shows the 1998 18Z observation of temperature at SFO, and the NCEP 18Z reanalysis at the ocean point just to the west of SFO, and the NCEP 18Z reanalysis at the land point just to the east of SFO. |
A neural network and linear regression technique are used to predict the difference between the 18Z ob and the 18Z reanalysis at the ocean point. The year 1998 is set aside for a test of the prediction system. Also 1/3 of the data records chosen at random and set aside as a verification data set. The remaining 2/3 were used as a training data set. The predictors for the 18 Z observed SFO 2 m temperature are:
All variables have their mean subtracted and and are scaled by (meaning divided by) 5 times the calculated variance.
 |
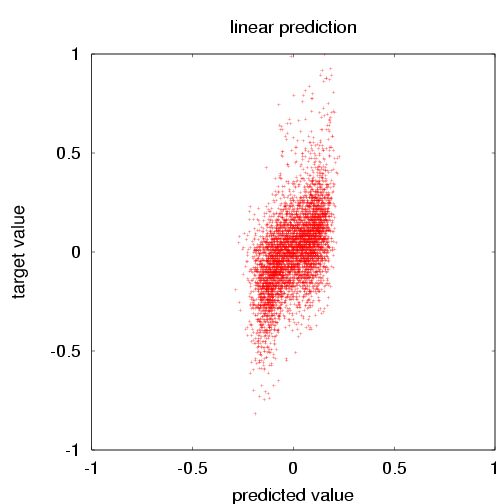 |
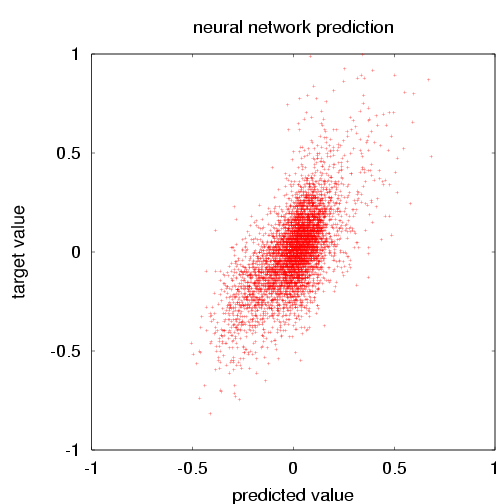
| The SFO surface air temperature vs. the neural network prediction for the verification data. The mean square error (error=prediction-target) is 0.0231. The mean square of the target is 0.0417. The skill score is thus 0.446. (For the training data, those numbers were 0.0218, 0.0391 and 0.442). | The SFO surface air temperature vs. the the singular value decomposition prediction for the verification data. The mean square error (error=prediction-target) is 0.0296. The mean square of the target is 0.0417. The skill score is thus 0.290. (For the training data, those numbers were 0.0283, 0.0391 and 0.277). |
Having trained the linear and nonlinear network, we examine the prediction for just one year: 1998. For that year, the skill score with the neural network is 0.38. The skill score for linear regression (svd) is 0.31. A casual inspection of the plot below shows that both methods offer a similar improvement for many of the events. But there are a few events where the neural network is better, and a few where SVD is better. There are quite a few events where boths methods fall short.
Half of the columns of data were ignored. Can you make a better forecast model? I was not able to reduce the error with the verification data by either expanding the size of the hidden layer or by using more predictors. There are of course many more predictors that could be considered, rather than just the 12 Z column of reanalysis data above SFO. Warning: If you make a big input vector, or big hidden layer, be very careful of over-fitting. The symptoms of over-fitting is that the error for forecasting with your training data is much less than for the verification data. "Over-fitting" is sometimes referred to as "fitting to noise".
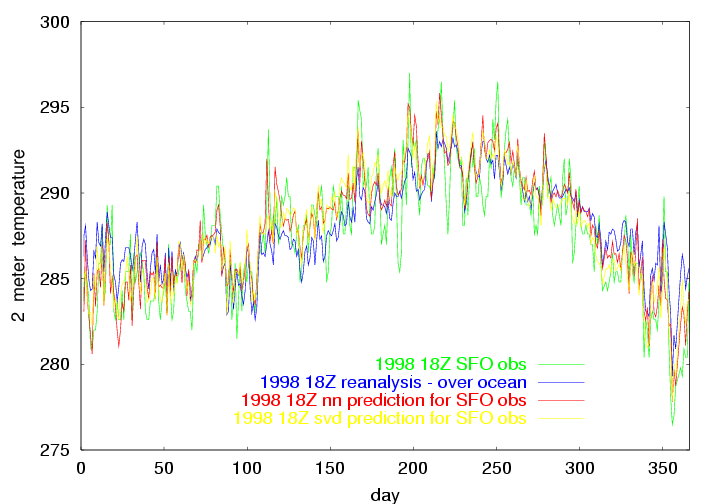 |
The above image shows the 1998 18Z observation of temperature at SFO, and the NCEP 18Z reanalysis at the ocean point just to the west of SFO, the neural network prediction for the SFO obs, and the SVD prediction for the SFO obs. |