A Regular Perturbation Expansion
for

Solution of with
y(0)=1.
We seek a solution of form

Logan 1.4 on page 50 (1st edition).

Here is the proposed series solution:

In[1]:=

Out[1]=

In[2]:=

Out[2]=

Here is the equation with the proposed perturbation solution:

In[3]:=

Out[3]=

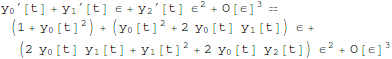
With the O[ε] symbol, the LogicalExpand does a powerful step:

In[4]:=

Out[4]=

Here is another way to look at it:

In[5]:=

Out[5]//TableForm=

Here is the ODE for :

In[6]:=

Out[6]=

...and it's solution:

In[7]:=

Out[7]=

Here is the ODE for , making use of the known solution for :

In[8]:=

Out[8]=

Here is the solution for :

In[9]:=

Out[9]=

In[10]:=

Out[10]=

In[11]:=

Out[11]=

In[12]:=

Out[12]=

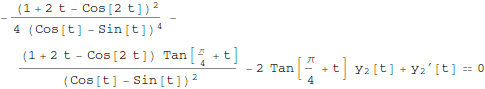
In[13]:=

Out[13]=

Now convert these replacement rules into approximate solutions, of increasing O[ε],
that we can plot:

In[14]:=

Out[14]=

In[15]:=

Out[15]=

In[16]:=

Out[16]=

In[17]:=

Out[17]=

In[18]:=

Out[18]=

In[19]:=

Out[19]=

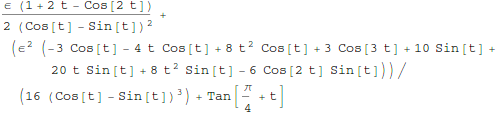
Test these functions:

In[20]:=

Out[20]=

Lucky for us, we can find the exact solution:

In[21]:=

Out[21]=

and here it is as a convenient function:

In[22]:=

Out[22]=

Let's test it:

In[23]:=

Out[23]=

In[24]:=

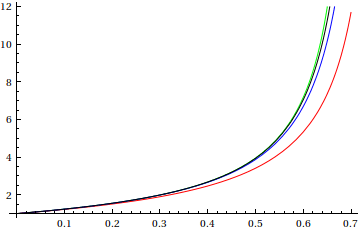
Here we plot the exact solution (green), the (red), (blue),  and (black).

In[25]:=

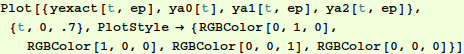
Out[25]=

Created with Wolfram Mathematica 8.0